Самое большое число в мире.

Сразу же найдутся люди, которые скажут что это "+∞",т.е. "плюс бесконечность".

А вот нифига подобного. Бесконечность в математике это понятие, концепция, а не какое-то конкретное число. С ней можно работать с точки зрения математического формализма, но невозможно определить точное значение (помните, назови целое число и прибавь к нему единичку - повторяй пока жив/существует_вселенная - так и познаешь что такое бесконечность).

Ну что же, будем разбираться с конкретными значениями больших чисел. Для начала возмём общепризнанную шкалу названий десятичных множителей (ну привыкли мы к десяти пальцам на руках, потому и система счисления десятичная):

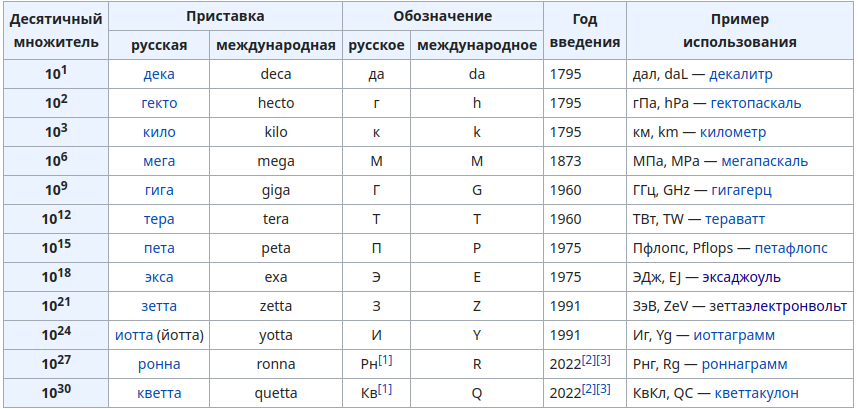
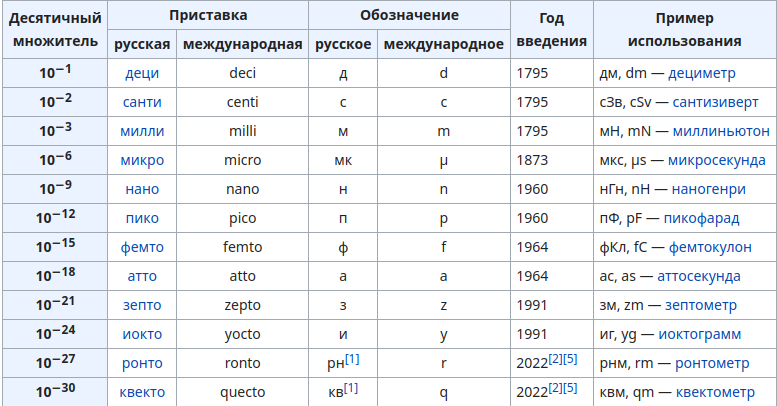
Эти приставки стандартизированы по СИ, но мы-то понимаем, что числа могут быть намного боельше.

Естественно эти приставки не в полной мере удовлетворяют наши потребности. Та же физика (наука наблюдательная) запросто оперирует величинами, вроде 6,626 070 15⋅10^-34 кг·м2·с−1 (Дж·с) (постоянная Планка).

Конечно народ напридумывал другие величины, вроде:

• 100*10^78 - сто квинвигинтиллионов (не в системе СИ) — предполагаемое количество атомов в наблюдаемой Вселенной.
• У всех на слуху естественно googol - 10^100
• 10^170 - число позиций в китайской игре Го.
• Гуголплекс (от англ.googolplex) — число, равное 10^googol (десяти в степени googol), то есть 10^10^100

Ну да ладно. Пока я был в стадии сперматозоида (и то не факт) во всю работал выдающийся математик и программист Дональд Эрвин Кнут. (как же я гонялся за его трёхтомником "Исскуство программирования", но даже первый том был мне, студенту, не по карману). Он подумал, а действительно, как записывать о-о-о-чень большие числа. Числа, у которых показатель степени той же десятки не влезает в тетрадь. И придумал "стрелку Кнута":

"Возведение в степень. Если мы пишем 3^4, то имеем в виду, что число 3 мы умножаем на себя 4 раза. Получаем 81.Здесь в дело вступают стрелки Кнута. В этой нотации 3↑4 — это то же самое, что и 3^4. Самое интересное начинается, когда мы добавляем несколько стрелок подряд."

И далее

"Тетрация. Если мы пишем 3↑↑4, то имеем в виду, что число 3 мы возводим в степень себя же 4 − 1 раза. Для этого мы сначала возводим 3 в степень 3, получаем 27. Затем возводим 3 в степень 27, получаем 7 625 597 484 987. И наконец возводим 3 в степень 7 625 597 484 987 — получаем настолько большое число, что записать его привычным способом просто невозможно. Представьте, что мы заполнили всю наблюдаемую Вселенную песком и каждую секунду заменяем все эти песчинки новыми. Если мы будем заниматься этим в течение 10 миллионов лет, то общее количество песчинок, побывавших в нашей Вселенной-песочнице, и на одну миллионную не приблизится к числу 3↑↑4. Но и это не всё."

Т.е. мы можем описать таким образом реально гигантские числа в короткой записи.

В 1977 году американский математик-любитель Мартин Гарднер выпустил статью, в которой описал число Грэма. Что самое интересное, это число возникло не с потолка, а в результате решений в области теории Рамсея (жуть жуткая и мне непостижимая). Что самое интересное, это самое большое число, которое использовалось в к-либо научных работах вообще. Через стрелочки Кнута оно выражается так:

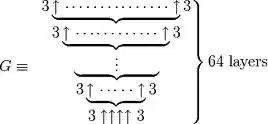
Не буду упоминать число Райо, т.к. суть этой формулировки я понять не в состоянии и тем более не смогу описать доступным языком, но определение формально чистое.