Вроде с периметром прямоугольника всё просто - перемножили стороны - получили площадь. Ладно, берём круг - снова перемножили - и получили однозначное отношение периметра к площади.
Всё енто хорошо, пока в дело не вступает фрактальная геометрия. Там появляются дробные размерности. Вроде чего проще: точка - нулевая размерность, линия - одна размерность, плоскость - две размерности.
И вот, в достаточно древние времена, один шведский математик по фамилии Кох, (не путать с немцем - Кохом, который научился культивировать сибирскую язву.) в 1904м году решился поиграть в рекурсию с линейкой и угольником.
Однако он оказался достаточно вумный и описал свои фигурки математически.
Фишка в том, что периметр данной фигуры, строящейся рекурсивно, замкнутой (к сожалению не дифференцируемой, т.к. состоит исключительно из вершин пиков, т.е. функция не гладкая => не имеет производных) бесконечен.
А вот площадь кривой Коха конечна.
Вот я Вам мозги в тяпницу запудрил - наслаждайтесь наглядной и красивой геометрией:
В прошлом посту я показал, что на самом деле, в природе, нет никакой связи между периметром и площадью фигуры. В качестве примера была снежинка Коха. Вроде пример надуманный - и всё это просто игры математиков. А вот нифига. В природе эти фракталы встречаются почти везде.
Самый популярный и наглядный пример природного фрактала - лист папоротника
Глядя на фотку выше математик Майкл Брансли решил описать его математически (делать ему больше нечего что ли?) и, у него получилось(более-менее точно):
Один в один же папоротник
Та же береговая линия острова. Чем точнее будем вычислять периметр острова тем тоскливее нам будет (периметр таких фракталов обычно стремится к бесконечности).
Но у фракталов есть ещё одна характеристика - размерность.
Например у математической (а не ручкой поставленной) точки размерность равна нулю, у линии - единице, у плоскости двойке, у куба - тройке, а вот у сферы снова двойке (это Вам для разминки мозгов), в то время как у шара - привычная тройка. Т.е. на линии мы можем взять точку отсчёта и обозначить положение на линии одной координатой, на плоскости уже двумя, у куба - три(ширина, высота и длина) и т.д.
А что же с размерностью у фракталов?
Думали-думали и придумали. Решилм использовать фрактальную размерность. Её начали использовать для определения сложных объектов (не обязательно бесконечных фракталов). Фообще слово фрактал (fractured) в математике означает "дробное". Определили енту величину как меру сложности подобных структур. Как оценить енту меру-то? Ведь математикам нужно конкретное число, а не то что один сказал - "просто", второй "сложно", третий "пойдёт"... Решили, что на определённом массштабе определяется количество отдельных элементов и как это число меняется при уменьшении массштаба.
Математически выглядит так:
D — фрактальная размерность, показатель сложности и структуры объекта;
log(N) — логарифм числа элементов, необходимых для
покрытия фрактала. По мере уменьшения масштаба размер элементов
уменьшается, а их количество увеличивается;
log(S) — логарифм обратного масштаба (размера элементов). Чем меньше элемент, тем больше их требуется для покрытия всей структуры.
А формула простое соотношение D=log(N) / log(S).
Для той же снежинки Коха
GIF
Сначала просто, а потом просто красиво
Снежинка строится на отрезке, который делится на три равные части, затем на средней части создается «пик» в форме равностороннего треугольника без основания. В результате каждый исходный отрезок заменяется на 4 меньших, и так далее. Получаем, что S = 3, N = 4, а размерность log(4) / log(3) ≈1.261859507...
Вот такие чудеса, вомбатяне, оказывается имеются и дробные размерности, причём в самой природе.
Офигительный вопрос на который большинство ответит: "Одно и тоже". А вот нифига. Масса = это просто число, оно определяет как много вещества находится в данном теле. Именно Масса определяет количество энергии, которое надо затратить на разгон одного киллограмма до скорости в 1 м/с. Второй закон Ньютона все помним? А что такое инерция?
Вот так масса и определяется.
А что такое вес? Вот стала моя тушка на весы и они показали 98кг веса.
А вот тут дъявол кроется в деталях.
Масса - та же моя тушка, это мера инертности, но не вес. Для силы, которая толкает массу до лампочки куда и как её двигать, т.е. величина постоянная и скалярная - не имеет направления.
А что же вес? А тут засада. Мы живём на Земле, у нас есть её притяжение (неравномерное по разным точкам планеты) и енто притяжение тянетмою тушку (в 100кг массы) вниз на весы, которые показывают 98.89 кг - потому как притяжение не равно единице (ну так сложилась система единиц у человеокв).
Есть такие Питерские весы (контору писать не буду (реклама же будет), но их стиль узнаваем во многих магазинах)
Так вот такими весами мы и торговали (обслуживали и ремонтили, пока контора жива была). Сразу после закупа эти весы шли на калибровку и гос-поверку. А всё потому, что в Питере сила притяжения ниже чем у нас - врали.
Ну раз есть сила, значит и есть направление приложения ентой силы. А чувствительному элементу на енто всё похер - он выдаёт величину, равную его "прогибу". Чем сильнее его нагибаешь - тем сильнее он возмущается.
Таким образом выходит, что вес величина уже не скалярная, как масса, а векторная - имеет направление. И зависит не только от массы тела, но и приложенной силы (для весов - сила притяжения в геоиде). Т.е. вес - это уже векторная сила. Т.е. 2й закон Ньютона - сила*массу. Земля тащит нас с ускорением 9.8, мы имеем массу 1кг, на весы и пятки ощущаем усилие в 1*9.8 = 9.8 ньютонов.
Очень похожие и схожие понятия, а вот разница дикая по смыслу.
Видосик с ютуба, но как же хитро придумана игрушка - реально завораживает. Прекрасный подарок своему начальнику, что бы его раздражать звуками падающих шариков, не правда ли?
Что больше всего нравится - так то, что автор этой вещи дал ютуберу всё что он хотел по ентой вещи, а ведь реклама наверняка: "китай вечно прыгающий метал" или "дерево прыгает шар"
Честно говоря я впервые о таком услышал. Но ента хрень реально продаётся.
Скриншот с сайта конторы, логотип которой в правом верхнем углу. Надеюсь и не реклама и авт. права на кусок таблички указал...
Озадачился, а чё енто за хрень? И правда ли послать шиномонтажников куда подальше - с помощью гранул делать всё самому (две монтировки и навык)? Долго гуглил - кто что говорит. Естественно продаваны и производители гранул 146% дают на работоспособность ентой вещи.
В результате наткнулся на видос с ютрупа и стало понятно что к чему.
Как по мне - хрень полная. Я должен разогнаться до оч. большой скорости что бы физика ентого эффекта начала работать, но как только остановился - хана, будет ещё хуже... Чем-то напомнило ферриты:
Ловите. Причём такая фигня и сейчас происходит, я как инженер говорю. Здравую, полезную идею начальство превращает в абсурд, и в результате ты же и виноват...
А что такое "пердят" спросят субботние вомбаты? Да очень просто - это так называемый "прострел", когда бенз догорает уже в выхлопной трубе, а не в цилиндре. Всё из-за того что "гоночнЕкам" абсолютно насрать на жор бенза и целостность вылопа (он у них наверняка самопальный из нержавейки в 3мм, а не как у меня на жигулях полтора миллиметра железа).
Вся фишка в том, что если обороты низкие (не в отсечку) - топливо сгорает в цилиндре. А вот если нагрузки нет и обороты идут в "отсечку" (искуственное ограничение оборотов за счёт перекрытия топлива и отключки зажигания дабы спасти дкигло от "кулака"), то выгорать ему приходится в выхлопной трубе, т.к. есть инерция системы питания двигла.
На гражданских авто - причин много. По карбюраторам если (это то что я знаю), то в певую очередь карб богатит смесь, второе - угол зажигания на трамблёре.
Я офигел от подхода решения этой задачи. Так замаскировать банальное решение - это надо уметь. Честно говоря, умение решать подобные задачи очень сильно развивает способность неординарно, необычно мыслить. Наверное именно поэтому у японцев частенько появляются прорывы в технике.
Смотрите и наслаждайтесь занимательной математикой:
Это в лайфхаки надо. Реально. Ёжика, если только ты его сам же, как котёнка, не вырастил, крайне сложно раскрутить из "клубка защиты".
У нас был в доме дикий ёжик, однажды он насадил себе на лапу к-то значок, которые я в возрасте около 10 лет пытался собирать...
Т.к. ему было больно, но он упорный, то по ночам звенел по всей хате очень знатно. В свою "коробку", которую устроила мама для него под моей кроватью он вообще не заходил, а ныкался где-то в нашем деревенском доме. Мест заныкаться там море.
Нам енто надоело - спать же не даёт - мало его "тыбыдыма", так ещё и значком звякает.
Мне ультиматум - делай что хош, но найди эту звякающую заразу. Нашёл, непомню где уже, но тот тихо мирно в "клубке" спал. Брал его голыми руками - приловчился к тому времени (это как йоги на гвоздях спят - принцип тот же).
Притащил к маме, та мне на руки полотенце, сама руки полотенцем обмотала и начили этот "клубок" разворачивать для лечения. Было не просто - зараза весьма сильная и иголками запросто прокалывала полотенца. Искололись, но развернули в лежачее положение. Там он уже сдался (видать структура мышц такая - не успел скукожится - хана). Лапа со значком намотала на себя всю хрень,, что валялась там, куда рука мамы с тряпкой не могла дотянуться, лапа загноилась. Естественно сняли значок, выдавили гной, обработали йодом и напихали в ранку стрептоцида. Забинтоват не вышло (рулончика лекопластыря небыло, а бинтом такую мелкую лапку не получалось). Напомню - это было в середине 80х годов в деревне. Ну и отпустили его. После этой процедуры для повторного осмотра я найти его не смог...
Он ещё где-то с недельку подыгыдымкал по ночам и исчез.
А тут увидел прикольный лайфхак, как раскрутить скукожившегося ёжика. Мэ до этого не додумались:
Красивые и необычные. И да, это не “воображение художника”. Видосики сделаны из толп фоток, которые американские марсоходы регулярно шлют на Землю.
Спёрто с фейсбука
А вся фишка такой раскраски неба естественно кроется в атмосфере Марса. Во первых она сильно разряжена, по сравнению с земной, во вторых в ней много пыли содержащей окислы железа, потому и рассеивает свет совсем иначе. Днём небо в рыже-красноватых тонах (логично, ведь Марс это “красная планета“), а вот закаты и рассветы в голубых тонах. Просто какая-то противоположность земному небу.
В этом 30-секундном видеоролике, имитирующем заход солнца над марсианским горизонтом, используются изображения с панорамной камеры (Pancam) марсохода NASA Opportunity. (c) гугло-переводчик
И да,. Я не про коктейль, который не видел в КБ и Бристоле моего "Лангедока" уже 100 лет. Смотрите и наслаждайтесь лёгким юмором от русского негра афроамериканца.
Классика жанра. Он ещё хинкали не пробовал...
Игра слов, но прикольно.
А жене понравился хлеб-гриль, для американцев это как для татар чай... Жаль что сейчас ей почти ничего нельзя.
А что, "холодец в кармане" - выглядит прикольно
Ну и вишенка на торте... И да, после этого "кваса" за руль лучше не садиться - не дай бог остановят...
Вчера (28.05.2026) на Мысе Канаверал, штат Флорида проводились огневые испытания ракеты-носителя тяжёлого класса New Glenn. Грубо говоря так называемый "прожиг" - тестовый запуск двигателей без попыток оторвать ракету от пускового стола. Испытания провалились, но красиво. Пострадавших нет, пусковой стол и сама ракета естественно уничтожены, общий ущерб оценивается около 4 миллиарда долларов США.
Кто-то перезалил новость на ютуб, с самого euronews видос не грузится.
это отрывок с рэддита
Ну, как говорится: "отрицательный опыт тоже опыт", надеюсь Безос допилит ракету до надёжности наших Союзов и пр. Зато красоту показали в реале, а не комп. эффекты в фильмах...
Индюки. Мы их держали в деревне - реально отморозки. Только пинок сапогом в зоб помогает - если промазал - заманаешься “отпинываться”….
Белки. Про них ходят легенды, но на самом деле видел их только из далека.
Страусы. Как-то делал доклад в школе по предмету “Природа” (в следующем классе, о докладе про Варана я как-то уже писал тут). У них реально мощнейшие лапы.
Бакланы - отдельная каста. Даже в тюряге.
Ну и про иглоукалывателей так же, вроде не постил “Матюгальника“
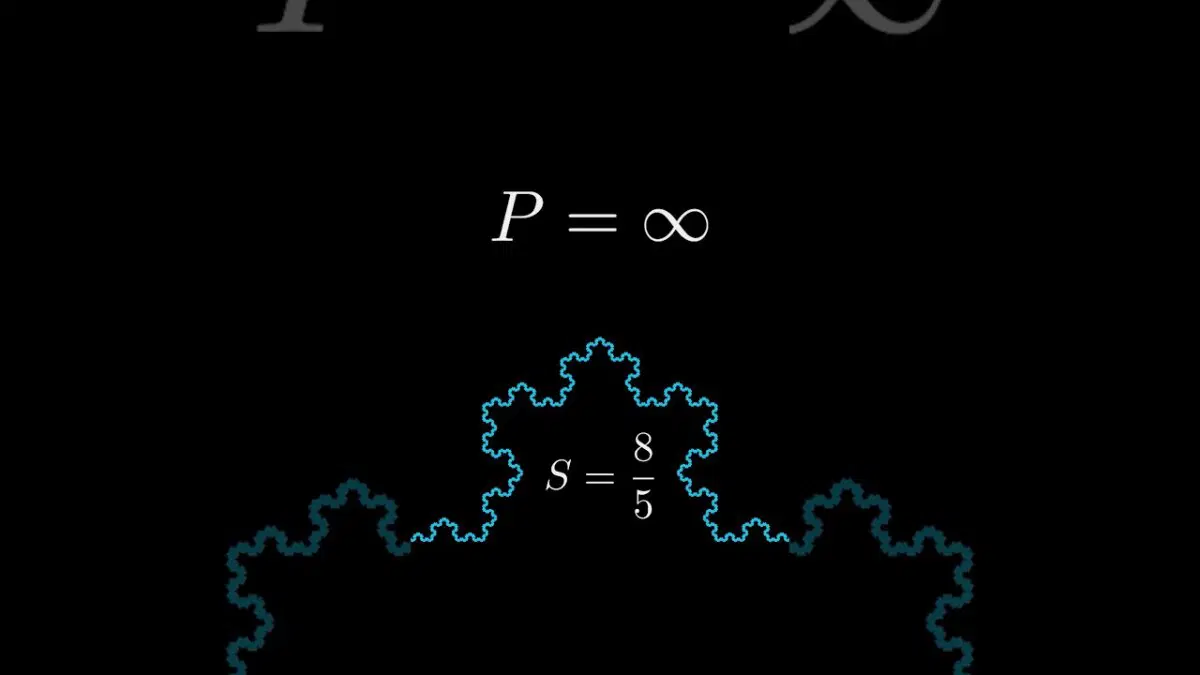
Комментарии