В стпоительных трендах сейчас диджитал-рулетка
Встроенный лазер идеально отмерит вам нужный отрезок вплоть до миллиметра.

Встроенный лазер идеально отмерит вам нужный отрезок вплоть до миллиметра.

Хеллоу, уважаемые.
Как некоторые могут догадываться, я люблю измерять всякое. И чем мельче - тем интереснее. В этот раз решил наступить в говно. А именно, купить профилометр 296. Что это такое? Это прибор, который с помощью древнесоветского шаговика двигает щуп на заданную дистанцию, собирает с него инфу с помощью тензорезисторов, пересчитывает и показывает шероховатость поверхности. Щуп представляет собой тонкую и короткую алмазную иглу, подвешенную на балке, которая поворачивается на шарнире. Соответственно, за счёт острого острия щуп может улавливать микрорельеф плоскости (речь идёт о субмикронных величинах). Вощем, купил эту хреновину, а оно не работает. Что естественно, если хранить прибор, спизжженный в НИИшке в луже. Долго ли коротко ли, один хороший человек согласился помочь с ремонтом. Даташитов на эту хтонь, ессесно нет, схем - ноль, внутри какие-то античные макросхемы. Ну вощем это всё он расковырял и починил довольно быстро, а вот с приводом - который таскает иглу туда-сюда - как раз и засада. Там всё закисло, заржавело и обрыбилось. А значит что? Значит, я должен сделать как новое. Поехали.

Короче, отмачиваю всё в керосине и, стараясь не протерять винтики, разбьираю и сразу чищу латунной кордщёткой и скотчбрайтом.


Поскольку ржавотина была не везде поверхностная, а хочется всё таки сделать максимально неплохо - решаю отпесочить всё это и переворонить.

Ну и переворонить, ессесно. В таком виде оно поржавеет через пару дней.

Ну вот. Куда лучше. Можно собирать.


А вот на этапе сборки основания случилось страшное... там линейные подшипники стоят, в них шарики 3мм. Ну и ессесно, один шарик ускакал. Курвёныш.

Пришлось купить мешок новых.

Ну и собсна, результат.


Явно же ту би континуед. Хоть процесс вялотекущ и идёт уже года два, если правильно помню, но обязательно закончится когда-нибудь. :)
А в целом, если интересно наблюдать за железяками - металлический онлифанс (ссылка в профиле) как бы говорит "заходите к нам на Рагнарёк". Железки и угар есть, а вот, скажем, рекламы всякого говна... или не говна... короче, никакой рекламы нет.
Точнее, о прикидке, насколько плоское - реально плоское.
Задача какая: есть некоторое к-во плит притирочных, разметочных и поверочных разных форм, размеров и качества. А также есть желание иметь на хозяйстве хотя бы одну плиту реально класса 0 или 00 (для тех, кто не в курсе, это когда на размере грубо 600х400 неплоскостность составляет микрона 3). А как померить? Вариантов есть несколько, но именно для прикидки качества плоскости решил изобрести вот такой приборчик. Плоскомер.

Почему "изобрести"? Потому что таких больше нет. Ни на ютубе, нигде. Есть Repeat-o-meter, но он ваще по другому устроен и куда более громоздкий.
Итак, что из себя представляет мой плоскомер. Вертикальная плита из калёной до 36-42 HRC стали 40Х, в которой прорезано окно так, чтобы толщина перемычек, соединяющих правую часть основы и левую, подвижную часть были не толще 0,5мм. Таким образом получается шарнир, работающий в одной плоскости. Дальше это всё ставится на 4 точки, выполненные из круглых резковых вставок из твердосплава. Ну и максимально шлифуется. Погнали делать. Сперва на эрозии режу основную пластину и ножки.

Во, кайф. Серловка и резьборезие оставлю за каждром, ибо это и так все умеют. Дальше у нас запеканка:

И закалка. Ну и потом отпуск, ессесно.

Теперь шлифовка на плоскошлифе.

Зашибись вроде... Пока суть да дело, эрозия вырезала консоль крепления индикатора. В данном случае - соточник (чисто попробовать), а ваще сюда ставится одно- или двухмикронник.

После неплодолжительной сборочки получается вот так:

Особо чоткий зритель может видеть позади будущего шарнира - пластину-арретир. Она жёстко соединяет измеряющую часть и основание, чтобы эти сопливые 0,5 мм не согнуть и не сломать.
Теперь приделываем твердосплав:

Ну и после нанесения лазерной маркировочки, изделие готово.

Покатал по имеющимся плитам, получается, даже после шлифовки у меня плита заходит в нулевой класс. Я на канале видео выкладывал. По плите 400х400 между максимумом и минимумом если правильно помню - 4 микрона. Хорошо. Но теперь желание проверить насколько верно работает сам прибор. А для этого нужна плита 00 класса, желательно гранитная и на краску приложить ту, что уже померил. :) Вощем, если уж залез в точные измерения, вылезти оттуда сложно, ребят. Не повторяйте моих ошибок. А то сейчас уже и оптикатор с разрешением в 0,1 микрона есть и пластины интерференционные, которые в правильном свете порядка 350 нм показывают. Ужас.
А если кому интересна металлообработка прям в режиме онлайн, без рекламы, политоты и прочего говна, тому вот сюда:
Всем здравствовать!
В рамках
события недели, а так же в рамках борьбы со скукой (на работе совершенно нечем
заняться, да и вам, надеюсь, будет интересно) решил я узнать, сколько это - один миг.
Как выяснилось, этот термин применяется как единица измерения. Да-да, впервые слово
«миг», а точнее его английский аналог «Jiffy», предложил использовать Ньютон.

Уж и
пошутить нельзя?
На самом деле этим
учёным был Гилберт Ньютон Льюис (англ. Gilbert Newton Lewis). Американский
физический химик.

Дядька был
выдающимся учёным, и как впоследствии выяснилось ещё и толковым
администратором. Как говорится: «Талантливый человек, талантлив во всём».
Ну, так вот, в 1926 году этот самый учёный и предложил использовать термин «миг»
для обозначения отрезка времени, которое требуется свету, чтобы преодолеть в
вакууме аж целый сантиметр. Знаете сколько это в секундах? Я тоже не знаю,
давайте посчитаем. Берём скорость света в вакууме (ок гугл) - 299 792 458
метров в секунду. И что дальше? Переводим метры в сантиметры 29 979 245 800
сантиметров в секунду, делим одну секунду на это значение и получаем 0,0000000000333564
секунды. Ленивые люди такие числа преобразуют в вид типа 33,3564 * 10¹²,
видимо лень ноли считать, ну или 33,3564 пикосекунды, если хотите. Главное, что
теперь миг не просто абстрактное понятие, а физическая величина.
А знаете чему равняется секунда? Правильно, 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного квантового состояния атома цезия¹³³ в покое при 0° К. Я без понятия как это перевести на человеческий язык. Так сколько же раз атом цезия¹³³ сделает переходов за один миг?

0,306633102372828 раз, т.е. он один переход делает за 3,261226502493274342 мига или за 0,1087827757077666562614888 наносекунды. Я не знаю, зачем мне эта информация, да и вам вряд ли пригодится, но пусть будет, как знать, вдруг захочется кого-нибудь поразить за праздничным столом, особенно после бокала шампанского.
Ладно, на сегодня, пожалуй, всё. До новых встреч!
P.S. хотел было доказательства привести из приличных журналов, в смысле про то, что Гилберт Ньютон Льюис действительно применил этот термин, но благодаря РКН, я не смог этого сделать. Могу лишь предложить англицкую вики статью.

Хеллоу, уважаемые. Сегодня расскажу хладную былину, как без регистрации и СМС повысить точность и всё такое, шоб получалось хорошо, а не как-нибудь.
Есть такая штука - зубофрезерный станок высокой точности, называется Pfauter RS-00. Он может резать как прямозубые зубчатые колёса, так и косозубые.

Однако суппорт станка даже при нарезке прямозубых шестерен должен быть наклонён на значение угла, указанного на червячной модульной фрезе. А там обычно что-то типа 3 градуса 18 минут, например. Можно этот угол не выдерживать, конечно... но получится плохо. Например вот так. Слева "правильно", справа - прососан угол наклона. Т.е. зубы есть, но кривые.

Для выставления угла суппорта обычно используется "китайский кубик". Ну а чо, просто и недораха, верно?

Есть только одно "но". Эти и большинство других китайских угломеров размечены в т.н. "новых градусах". Ну т.е. на фрезе указан, например, угол 3 гр. 20 мин., а на кубике 3,20 градуса. А это - разные вещи. Потому как угловая минута это 1\60 градуса, а новая угловая минута - 1\100. Херасе - чуть не в два раза короче! Можно, разумеется, пересчитать все углы в "новые" и посевить шпаргалку на станок... Но тут ещё одна проблема. Эти кубики имеют крайне низкую точность. Если для нарезки зуба типа м2, где глубина врезания 4,5мм и ваще зубы эпическиого размера, это ещё нормально, то модуль типа 0,4 - уже хотелось бы поточнее. Что же делать, спросите вы? Да всё просто. Берём подверстачный мусор, ставим на электроэрозионный проволочновырезной станок.
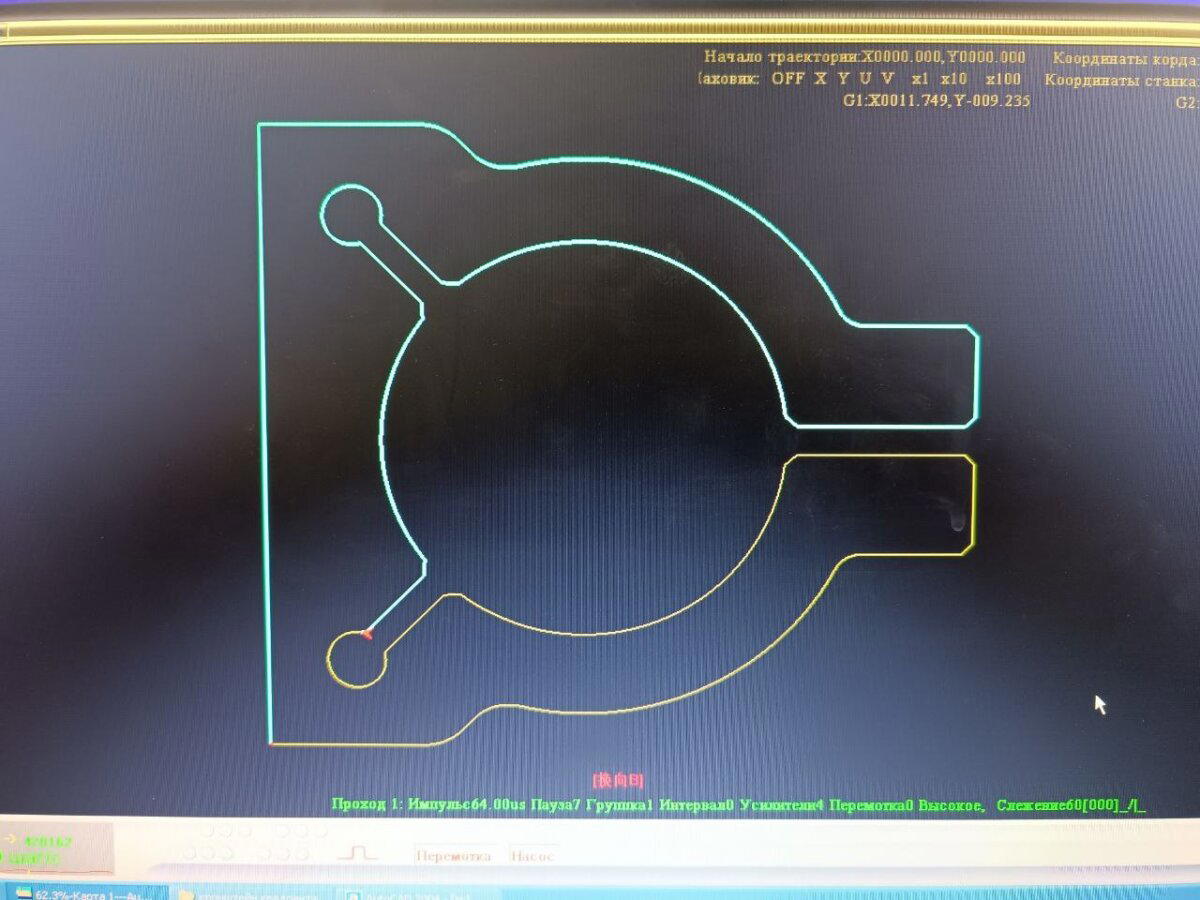
путём приваривания того и этого, а также шлоского шлифования на скалке на призмах, добиваемся плоскостности привалочной плоскости и её параллельности оси отверстия. Ну и напячиваем сверху Квадрант Оптический КО-1.

Размещаем сборку на хвосте суппорта... вообще, там желательно иметь маховик... но маховик у меня перенесён на вторую штатную точку крепления - на голову станка. Поэтому хвост свободен. А он точно соосен оси вращения фрезы. А нам только того и надо.

далее крутим морду квадранта пока пузырь не встанет в горизонт (разумеется, предварительно сам станок должен быть выставлен в горизонт по обеим осям с использованием брускового или рамочного станочного уровня с разрешением 0,02мм на метр)... и смотрим внутрь.

У нас две шкалы. На одной - сколько мы перешли за целый градус, на другой - сколько не дошли до следующего. Иногда удобно. Наебковой техникой (постукиванием резиновой киянкой по корпусу суппорта) выставляем суппорт на нужный угол, затягиваем и...

Чистый мёд! Заготовка крутится, лавэшка мутится. На изображении второй проход, вроде. Я даже мелкие модули режу как минимум в 2 прохода. И станок не напрягается и почище выходит. Кактатак.
Вся эта тема подробно и в онлайне описывается в телегоканале, каковой указан в профиле. Есличо - добро пожаловать.
Время — деньги. Иногда от точности наших часов может зависеть жизнь. Какие только технологии люди не использовали, чтобы точнее отмерять время.

Время от времени нам приходится корректировать свои часы, ведь они начинают отставать или спешить. Но есть устройства, которым нужно три миллиона лет, чтобы отстать от эталонного времени на секунду.
В классической физике время — это априорная характеристика, которая ничем не определяется. Это значит, что, по сути, человек сам придумал такое понятие, как время, и задал его характеристики. В частности, человек придумал такую меру времени, как секунда.
В Древнем Египте люди отмеряли время с точностью до часов: они делили день и ночь на 12 равных частей, которыми и оперировали. Позже в обиход людей пришли минуты, которые представляли собой час, деленный на 60 равных частей. Почему 60? Потому что так решили жители Вавилонии, которые даже день делили на 60 частей. Позже, с изобретением часов, люди начали отмерять время все точнее.
Так, в 1579 году швейцарский часовщик Йост Бюрги изготовил первые часы, которые могли отмерять секунды. Однако позже астроном Тихо Браге жаловался, что показания разных часов в его обсерватории отличаются аж на четыре секунды. Такая точность для ученого была неприемлемо низкой. Позже мастера начали делать часы с секундным маятником, который увеличил их точность. Но до сих пор не было понятно, что же представляет из себя эта секунда.
В 1956 году эту единицу измерения определили как «1/31 556 925,9747 доля тропического года для 0 января 1900 в 12 часов эфемеридного времени». Но спустя 10 лет — в 1967 году — это определение решили пересмотреть и по-новому описать секунду. В результате ученые пришли к принятому сегодня определению: «Секунда — это время, равное 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133».
Именно на принципе перехода атома между двумя состояниями построены самые точные часы в мире — атомные. Они состоят из двух частей: в первой происходят колебания атомов четко определенного изотопа, которые фиксируются приборами. Во второй части колеблется кварцевый кристалл с постоянной известной частотой. Сам по себе кварцевый кристалл можно использовать для определения времени, так как он колеблется с точно известной постоянной частотой.
Однако, через время стабильность кристалла может нарушаться и измеренное с помощью него время будет не таким точным. Поэтому во второй части конструкции атомных часов используют устройство для генерации атомных колебаний — механизм часов сверяет два значения и подстраивает показания кварцевого генератора под то, что показывает детектор атомных колебаний. В результате получаются часы, которые отклоняются от эталонного времени на секунду за три миллиона лет.
10. Дорога на Запад.
15.
Когда мы говорили про измерение базиса, уважаемый Netlog позволил себе усомниться в оценке точности измерения базиса вехами. И был совершенно прав. Тут "дьявол", как обычно, в деталях. Это текст про измерения, поэтому смело пропускайте его, если вас интересуют приключения. Они скоро воспоследуют в следующей части.
Я тут ступаю на тонкий лед, но все же хочу поговорить о том, какая это относительная вещь: точность, погрешность и их оценка до того как вообще ввели понятие средней квадратической погрешности (СКП).
"Геодезист верит только себе и только до обеда" - любил говаривать один из моих учителей, Юрий Евгеньевич Федосеев.
И каждому геодезисту (и вообще, любому техническому специалисту, чья судьба связана с измерениями) с первого курса вдалбливают: полученная тобой величина не имеет никакого смысла без оценки того, с какой точностью она измерена.
То есть, можно получить скамейку длиной в 1.0 м, измеренную с погрешностью в 0,5 м (это неприемлемо). А можно получить стол длиной 1.000 м, измеренный с точностью 1 мм, и это будет хорошо.
В 1730-е годы, о которых мы говорим, представление об оценке точности было. А вот устоявшихся и унифицированных процедур (вроде вычисления средней квадратической погрешности) - не было. Поэтому каждый творчески подходил к оценке своих измерений. И лично мне это особенно любопытно.
Кстати, я еще застала период, когда ученые мужи ломали копья: как правильно - среднеквадратическая погрешность или ошибка? Мол, если ошибка, то она должна быть систематической и намеренной, а мы говорим о случайных огрехах. Так или иначе, сейчас приняты сокращения СКП (среднеквадратическая погрешность), СКО (среднеквадратическое отклонение) и СКОш (среднеквадратическая ошибка, которую вы можете встретить только в старых учебниках).
Так вот, вернемся в наше Перу. Базис Яруки был протяженностью 7 миль (12 км). Много это или мало? Кассини во Франции работал с базисами длиной 6 миль (9,5 км) и 9 миль (14 км). Так что в Перу было в самый раз.
Каждая бригада имела три деревянных мерных вехи. Два-три раза в день длина вехи проверялась относительно эталонного туаза (1,9 м). Годен работал с оригиналом туаза, Буге - с копией, изготовленной на месте мастером Гюго. Сразу же в измерения вводились поправки за расширение (сжатие) вех.
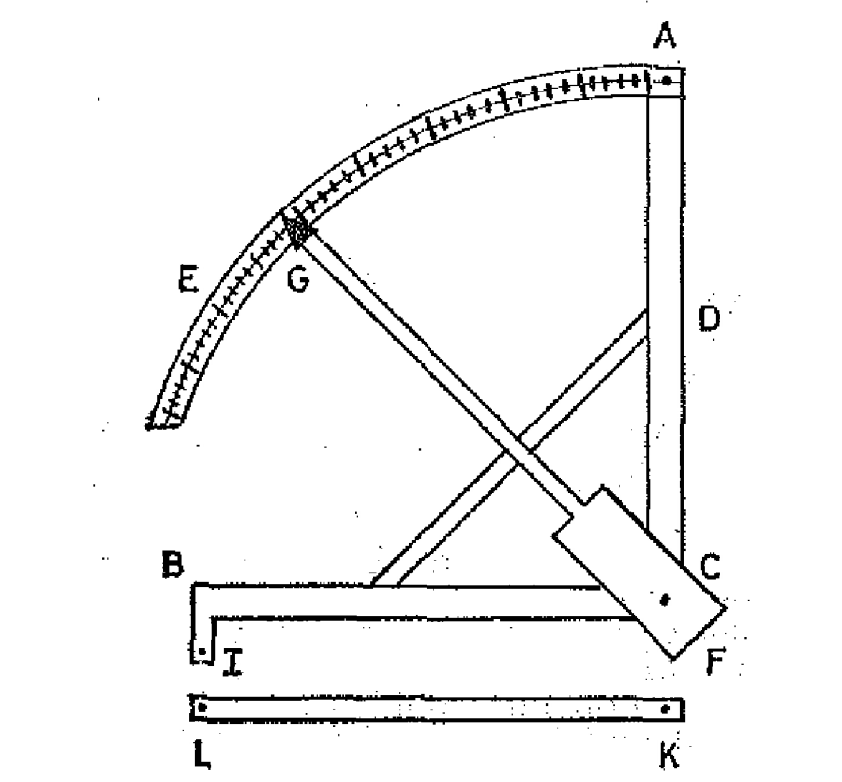
Cхема прибора, изготовленного мастером Гюго для сравнения вехи с эталоном. A.Lafuente, Delgado, La geometrizacion de la tierra observaciones y resultados de la expedicion geodesica hispano-francesa al virreinato del Peru 1735-1744.
После 3 ноября 1736 года две бригады сравнили полученные расстояния. Они отличались на 2 дюйма, 10 линий. Разница составила около 7 см при расстоянии в 12 км. Договорились принять за итоговое значение длины базиса 6272 туаза, 4 фута 3 дюйма, 7 линий. Именно эта информация и была отправлена в Париж.
Является ли это расхождение: 7 см на 12 км относительной погрешностью измерений? Как бы, нет. Это просто сходимость двух результатов. Может быть, просто повезло, может быть, ученые молодцы. Я в прошлом посте про базис предложила сравнение с погрешностью тахеометра (5-6 см на 12 км). Мне показалось это хорошей иллюстрацией к порядку точности работ.
Но тут есть и лукавство: а) это средняя квадратичкеская погрешность измерения расстояния тахеометром (а не сходимость результатов) б) никто десятки километров одним приемом тахеометром не измеряет.
Редуцирование базиса
До сих пор с базисом все шло у ученых отлично для их времени. Дальше каждый по-своему осуществлял вычисление горизонтального проложения (то есть, приводил линию к горизонтуна уровне Карабуро) Dk, а потом опускал на уровень моря Dm.
Зачем это делали? Затем, что и сегодня: все измерения в геодезии редуцируют, то есть опускают на единую поверхность (сегодня это эллипсоид, тогда, из-за его отсутствия - уровень моря). Только так, на одной поверхности, можно корректно сравнивать парижские измерения и экваториальные. На картинке ниже видно, что линия, измеренная на высоте вулкана Карабуро будет длиннее, чем та же линия, спроектированная на уровень моря.
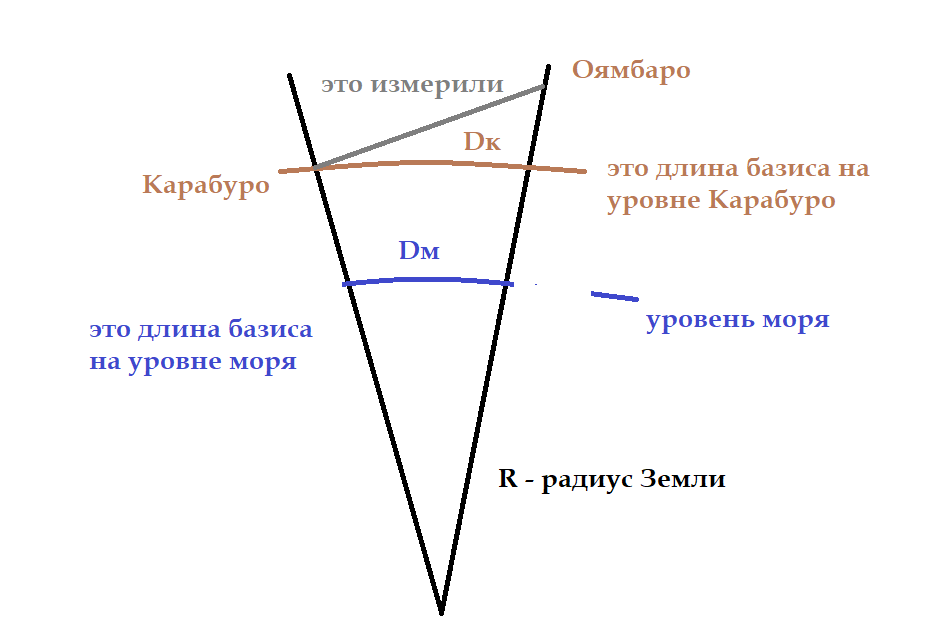
Серое — результат измерений. Dm — расстояние на уровне моря, с которым потом работали.
Чтобы осуществить все эти превращения, ученым нужно знать:
1) измеренное наклонное расстояние (ура, измерили!)
2) наклон измеренной линии (разность высот между Карабуро и Оямбаро).
3) Высоту над Карабуро над уровнем моря.
3) примерный радиус Земли (ха-ха, они как раз его и должны были определить!).
Как искали превышение Оямбаро над Карабуро?
Для этого у ученых были квадранты (метод называется тригонометрическое нивелирование).
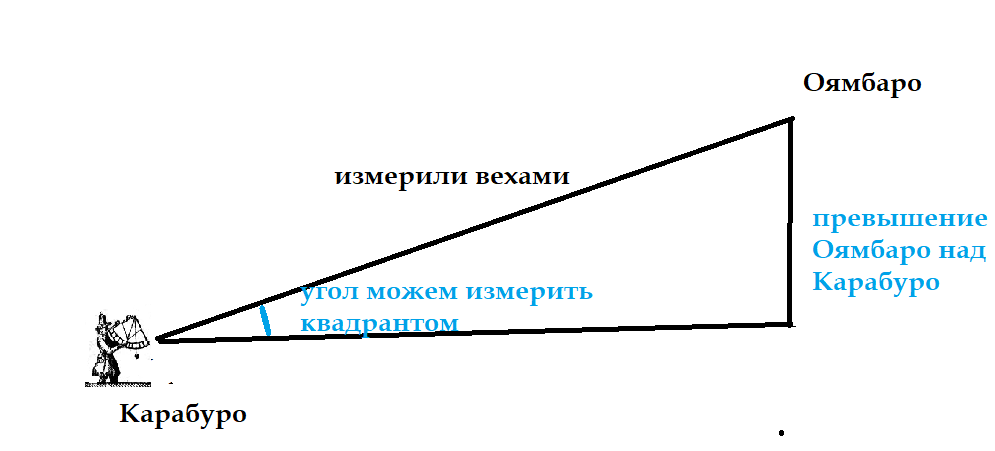
Мы знаем наклонное измеренное расстояние (гипотенузу треугольника). И можем измерить вертикальный угол (угол возвышения Оямбаро над горизонтом Карабуро). Горизонтальное проложение - это измеренное расстояние, помноженное на косинус вертикального угла.
Как искали высоты Оямбаро и Карабуро над уровнем моря? Это сейчас можно открыть Гугл карты. В тот 1736 году надеялись обойтись барометрическим нивелированием. На каждом из концов базиса замеряли давление ртутными барометрами.
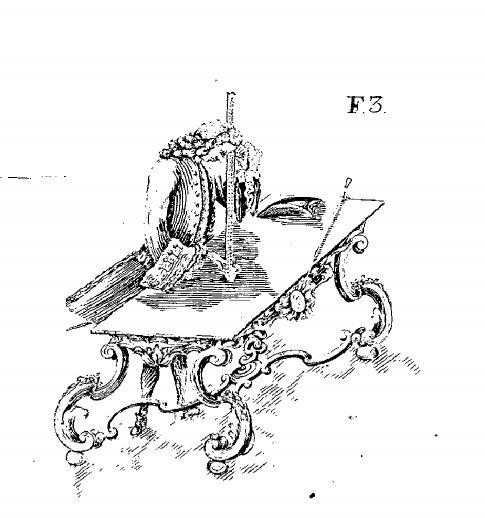
работа с ртутным барометром из "наблюдений" Хуана и Ульоа
Откуда брали примерный радиус Земли?
Лакондамин и Буге использовали большую полуось ту же, что и у Кассини (3255398 туазов или 6344770 м). Годен указал величину, предложенную Ньютоном: 3276500 туазов. Это это давало разницу порядка 10^-6 в измеренный базис (1,2 мм, незаметная величина).
Прочие расхождения
Были и другие математические преобразования, которые ученые решили произвести с базисом (причем каждый, исходя из собственных представлений о здравом смысле).
Интегрирование
Буге рассуждал, что измерена не линия, а ломаная, состоящая из отрезков, расположенных на разной высоте. И он выполнил интегрирование этих отрезков, чтобы уточнить линию, которая измерялась.
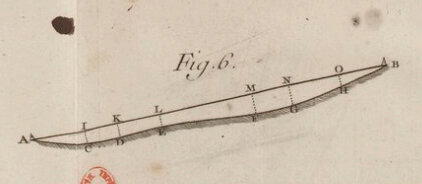
Учет рефракции
Поскольку превышение между Карабуро и Оямбаро определяли, измеряя вертикальный угол между ними, то большое внимание уделяли рефракции.
Рефракция - это отклонение луча света в атмосфере. Так что мы наблюдаем не настоящий угол между Карабуро и Оямбаро, а отклоненный. И значит, должны его исправить на влияние рефракции.
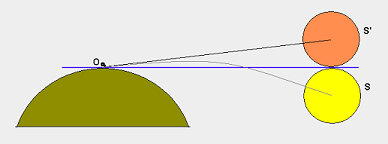
Атмосферная рефракция (Википедия). На самом деле солнце (желтое) находится ниже горизонта S. Но, поскольку луч отклоняется вверх, мы видим солнце S' — выше горизонта и измеряем не тот угол, на котором на самом деле находится солнце.
Эффект рефракции был описан в середине 17 века (Снеллом и Декартом независимо), но астрономы XVIII века упражнялись в том, чтобы определять влияние рефракции в любом удобном случае. Ее влияние зависит от высоты наблюдаемого объекта над горизонтом, а также температуры, влажности и атмосферного давления.
Годен действовал по следующей схеме:
Он сравнивал вертикальный угол (возвышение одного сигнала над другим) измеренный и рассчитанный эмпирически (по результатам барометрического нивелирования). И считал, что разница между этими углами и будет рефракцией. Величина получалась значительной (около 50”) и в которых измерениях была “отрицательная рефракция. Которую Годен называл “антирефракцией”). Физически это не имеет никакого смысла, но тогда кто же об этом знал?
Буге пошел другим путем. Он не доверял барометрам (ртуть частично испарилась, а купленная на месте обладала несколько иными свойствами). Поэтому отложил введение поправок за высоту над уровнем моря до 1740 года, когда предпринял двухмесячную поездку к побережью, чтобы тригонометрическим способом передать высоту от уровня моря на видимые горные вершины.
Лакондамин, описывает свой собственный ход рассуждений по поводу отыскания влияния рефракции на измеренные вертикальные углы, однако его результаты противоречат результатам Годена, так что он в конечном счете принимает за горизонтальное проложение базиса величину, близкую к той, которую подсказывал Годен: 6274 туаза 6 дюймов.
Контрольный базис
Чтобы проконтролировать “висячую” цепочку триангуляции, бригады наметили измерения контрольного базиса в южной части дуги в районе Куэнки.
Что такое контрольный базис? Это такая длина стороны одного из треугольников, которая будет известна из вычислений и из непосредственных измерений. Сравнивая вычисленную сторону с измеренной мы сможем проконтролировать качество проделанных работ.
К концу 1739 года атмосфера в экспедиции была такой неблагоприятной, что участники так и не договорились о месте для второго контрольного базиса. Годен и Хуан выберут один отрезок, Ульоа, Буге и ЛаКондамин - другой. С 1739 года у экспедиции два базиса и разные наборы треугольников, которые к ним ведут.
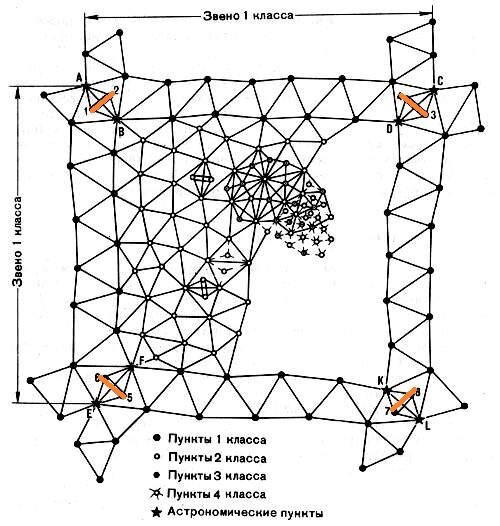
Картинка из интернетов со схемой триангуляции. Оранжевым отмечены базисы: их несколько, чтобы проконтролировать измерения в сети.
Годен и Хуан выбрали базис Гуанакуру-Баньос. На его измерение потратили 21 день. Створ проходил рядом с городом Куэнка, поэтому пришлось разрушить несколько стен и косвенно измерить расстояние через реку. Длина его составила 6 197 туазов 3 фута 8 дюймов, разница между вычисленным и полученным составляет 1 туаз - 1 дюйм (1,942м). При этом Хорхе Хуан считает, что цифры бы сошлись совершенно (?), если бы не разница температур на севере и юге в 8 градусов, которая привела к иному сжатию вех.
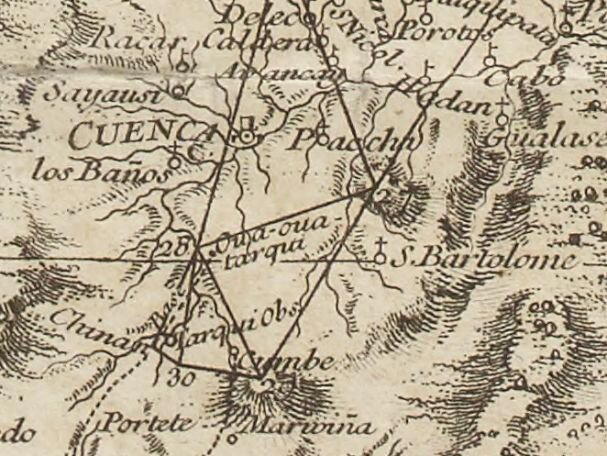
второй "контрольный" базис был где-то тут
Буге, Ульоа и Лакондамин выбрали долину вулкана Тарки. Базис был короткий: 6 миль длиной. Разница между вычисленным и измеренным составила всего 1 фут (30 см), что странно, учитывая то, что частично базис находился на болоте и вехи просто “плавали” по поверхности болота. Во время работы над этим базисом Антонио Ульоа был ранен молодым “метисом”. Но мы не будем подозревать ученых в "подгонке".

Окрестности Тарки (фото из интернетов), там был второй базис у Буге.
Итог: если первичные измерения у ученых сходились в пределах 7 см на 12 км, то проверка вычисленное-измеренное уже расходилось до 1,5 метров. Но они не афишировали этот факт в своих рукописях. Да и сами узнали это только в 1740 году (через три года после начала работ).