В первой главе мы с вами узнали, как и где создавались первые "шахматные автоматы", которые были всего лишь имитаторами программируемых шахматных роботов. Сегодня знакомство с первыми настоящими шахматными алгоритмами и программами.
© 2025 Константин Оборотов
=== Список всех глав
Глава 2. Как роботы научились играть в шахматы *
===
*** Глава 2. Как роботы научились играть в шахматы ***
Чтение советской и американской прессы 70-х годов прошлого XX-го века оставляет приятное послевкусие.
Конечно, нельзя было говорить о дружбе между СССР и США, но отношения явно улучшились по сравнению с послевоенными годами.
В американской прессе мелькают сообщения о смягчении давления американской бюрократии на Коммунистическую партию США. В частности, в 1973 году федеральный окружной суд в Аризоне постановил, что большая часть закона против американских коммунистов неконституционна, и Аризона должна допустить КП США к участию в голосовании на всеобщих выборах ("Блавис против Болина").
В советской прессе насмешки над убогим мещанским западным (в основном американским) образом жизни продолжались (в духе Михаила Задорнова "ну, тупые"). Но при этом явно начала изменяться эмоциональная окраска этих насмешек. Злая язвительная сатира потихоньку менялась на добродушный юмор с весёлыми приколами.
Вот мы читаем сообщение о нищем, который обитает на богатой парижской помойке. Ничего особо интересного в этом факте нет. Не было никакого секрета в том, что на этом Западе нищих огромное количество, как блох на бродячей собаке. Но именно в этом нищем была интересная изюминка. На своём плакате, ниже стандартного объявления "подайте плиз, кто сколько может жертве холокоста, бюрократии и бездушия", нищий сделал странную и наглую приписку "доллары США не принимаю".
Не знаю, придумал журналист эту хохму, или реально зафиксировал нечто подобное, но эта короткая заметка порождает у читателей множество мыслей, начиная от надежд, что долларовая долговая пирамида скоро рухнет до желания дать нищему полезный совет: "бери, дурачок, что дают, потом ненужное выбросишь".
Учёные экономисты по обе стороны океана начинают осторожно высказывать идеи о возможности "конвергенции" капитализма и социализма. При этом, в США должны усилиться социальные гарантии для трудящихся, а в СССР для "деловых людей" должны быть предоставлены возможности для полезных экономических частных инициатив (типа строительства личных дач и не только).
Самое главное, что в такой атмосфере о прямом военном конфликте не могло быть и речи. Решались вопросы о возможностях сотрудничества в разных областях.
В 1972 году в Москве председатель Совета министров СССР Алексей Косыгин и президент США Ричард Никсон подписывают "Соглашение о сотрудничестве в исследовании и использовании космического пространства в мирных целях". В 1975 году в рамках этого соглашения был реализован совместный полёт советского и американского пилотируемых космических кораблей со стыковкой на орбите (знаменитый проект "Союз - Аполлон").
Вот в таких условиях мирной конкуренции и делового сотрудничества СССР и США с явным желанием обеих сторон уйти от прямых военных столкновений в 1974 году состоялось грандиозное событие для всех любителей шахмат и прикладного программирования: первый в мире чемпионат мира среди шахматных программ.
Состоялось это мероприятие в Стокгольме во время конгресса ИФИП (IFIP, International Federation for Information Processing).
Лидерами в области шахматного программирования были американцы. В США было 50 действующих шахматных программ, во всем остальном мире (Европа + СССР) около 20. Также в США уже был богатый опыт проведения внутренних чемпионатов. Последний чемпионат США стал отборочным к первому чемпионату мира. Лучшими оказались программы: "Чесс-4.0", "Теч-2", "Хаос" и "Острич". Они и представляли США на этом турнире.
Что же касается нашей страны, то у нас в боевом режиме была единственная программа "Каисса" и ещё несколько программ в стадиях подготовки и перспективной разработки. Именно "Каисса" и представляла СССР на этом турнире. По итогам турнира "Каисса" заняла первое место и завоевала золотую медаль весом 110 грамм.
После окончания турнира "Каисса" в виде бонусного трека сыграла дополнительную товарищескую партию с лучшей американской программой "Чесс-4.0". После долгой и упорной борьбы партия завершилась вничью.
Насколько сильно играли лучшие компьютерные программы в 1974 году? Мне представляется, если бы они играли в сегодняшних (2025 год) турнирах для людей, например, на популярном шахматном сайте "ЛиЧесс", то изначально показывали бы рейтинг в диапазоне 1800-2000 в блице с контролем 5+0. Для сравнения сегодняшние лучшие гроссмейстеры показывают здесь рейтинги 3000+ или, как минимум, около того. А если бы обсчитывали рейтинги современных лучших компьютерных программ типа "Стокфиш" и "АльфаЗирро" при их играх с людьми, то мы увидели бы рейтинги 4000+ или даже 5000+. Короче, эти современные роботы били бы всех людей без малейших шансов для последних. Примечание. При условии взаимной честной игры, но это уже совсем другая тема.
После первого чемпионата разработчики упорно работали над усовершенствованием своих программ.
В 1977 году состоялся второй чемпионат мира среди компьютерных программ в канадском городе Торонто.
Наша "Каисса" приняла участие и в этом чемпионате. Уже в первом туре чемпионка преподнесла неожиданный сюрприз для всех, включая зрителей, своих разработчиков и присутствовавших на турнире гроссмейстеров и мастеров.
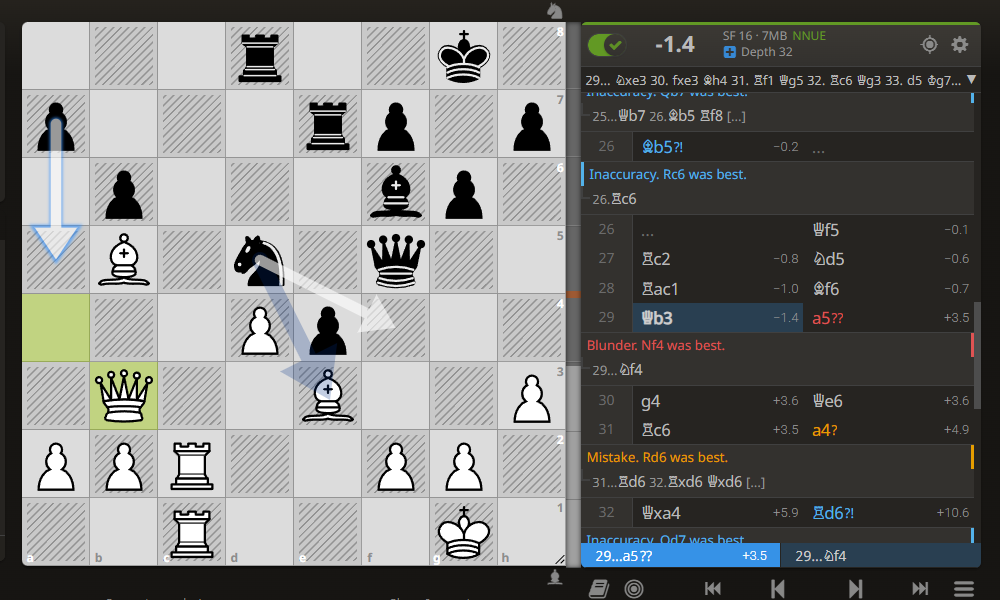
"Каисса" до этого игравшая неплохо в этой чуть лучшей позиции вдруг делает ряд странных ходов, начиная отсюда: 29. … а5?
30. g4 Фe6
31. Лc6 a4?
32. Ф:а4 Лd6
33. Л:d6 Ф:d6
34. Фа8+
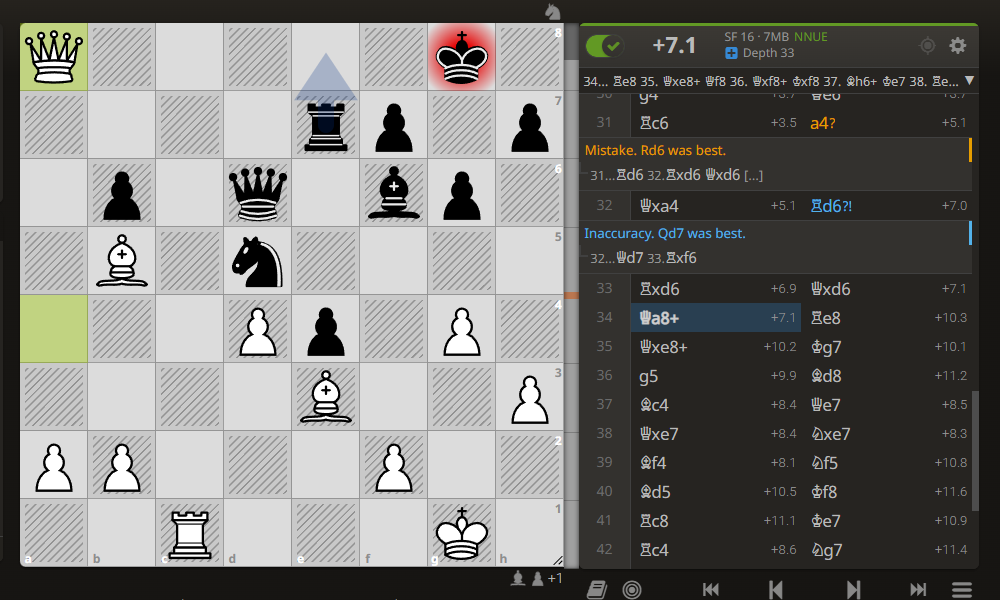
Но "Каисса" вдруг ставит под бой ладью 34. … Лe8 и затем постепенно проигрывает без каких-либо шансов.
После партии, когда Каиссу спросили, в чем дело, она объяснила, что ход 34. ... Крg7 гораздо хуже, чем сделанный ею ход 34. ... Лe8.
В доказательство "Каисса" показала такой вариант:
34. ... Крg7 35.Фf8+! Крxf8 36. Сh6+ Сg7 37. Лc8+
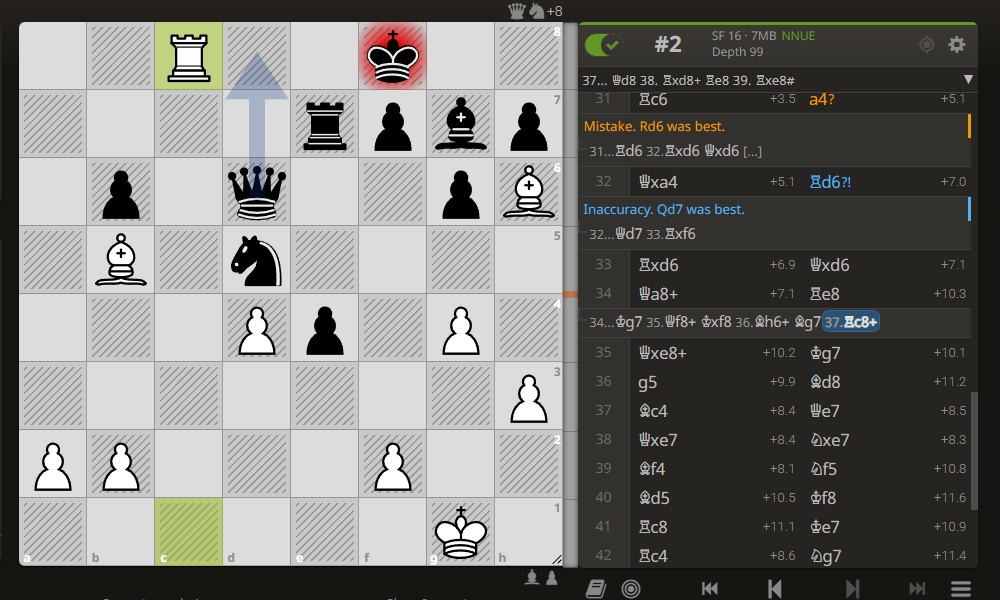
37. … Фd8 38. Л:d8+ Лe8 39. Л:e8X.
Специалисты, среди них были гроссмейстеры Ботвинник, Эдуард Ласкер, Ганс Берлинер, канадский международный мастер Леон Пиасетский эту комбинацию не обнаружили и объясняли народу этот заскок Каиссы "несовершенством шахматных программ".
В конечном результате турнира Каисса разделила 2—3 места с программой Duchess. Победила в чемпионате программа "Чесс-4.0".
До сих пор идут диспуты, а увидела бы программа Duchess во время партии этот выигрывающий ход 35.Фf8+
Далеко не факт, учитывая, ограниченность времени на обдумывание в турнирной партии.
В любом случае, если ход 34. ... Лe8 объективно сильнее (т.к. затягивал поражение на много ходов), то никто не будет спорить, что практических шансов больше у скромного хода 34. ... Крg7
Мне стало любопытно, а как бы в критической позиции пошла бы современная программа: 34. ... Лe8 или 34. ... Крg7 - ?
Я задал этот вопрос "Стокфишу" и получил ответ: 34. ... Лe8
Вот так!
Такие тонкие психологические моменты не понимали шахматные программы в 1977-м году, не понимают их они и сейчас, в 2025-м.
Возьмем этот факт на заметку, он нам пригодится для дальнейших рассуждений.
А как вообще роботы научились играть в шахматы? Точнее говоря, кто был их первым учителем?
Вообще говоря, много умнейших людей брались за эту интереснейшую проблему и решали её с разной степенью успеха.
Традиционно считается, что самым первым шахматным программистом в мире был Алан Тьюринг. В 1951 году он написал алгоритм Turochamp, с помощью которого машина могла бы играть в шахматы. Самое забавное, что это был чисто теоретический труд. У Алана не было компьютера, чтобы проверить свою программу на практике.
Тем не менее, его идеи были использованы другими учёными, а идеи тех, в свою очередь, новыми учёными, и вот, что мы имеем в сухом остатке.
Попробуем набросать примерный алгоритм игры в шахматы.
Что нам нужно сделать? Написать программу, которая умеет находить сильнейший ход в любой позиции.
Немного подумав, почитав разных полезных статей, становится ясно, что тут есть 2 принципиальных краеугольных камня.
Функция, которая оценивает позицию (оценочная функция).
Функция, которая как-то умеет определять максимальную глубину просмотра.
Давайте, попробуем набросать функцию, которая оценивает позицию.
Для простоты пока сделаем глубину просмотра равную одному полуходу и анализировать будем начальную позицию.
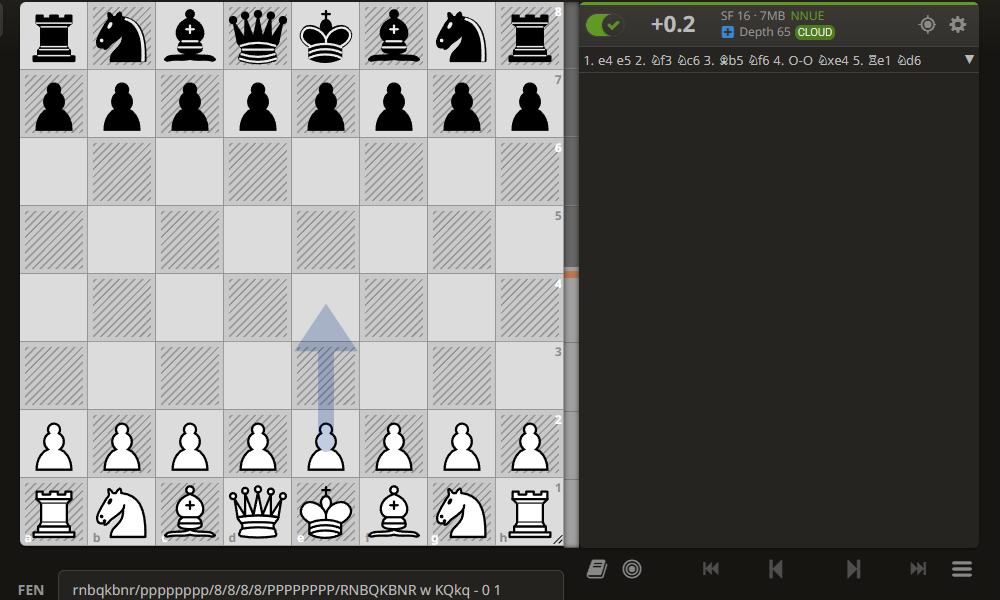
Опять же для простоты, чтобы не перенапрягать мозг, возьмем для оценки позиции следующие факторы (первые, которые пришли в голову).
Материал.
Количество пробиваемых полей (ударов по свободным полям).
Премия за очередь хода.
Проверка: нет ли кому-то вообще мата (пата) в данной позиции?
Материал Белые = 2Л*4.5+2К*3.0+2С*3.1+1Ф*9.0+8п*1.0=9+6+6.2+9+8=38.2
Материал Черные = 2Л*4.5+2К*3.0+2С*3.1+1Ф*9.0+8п*1.0=9+6+6.2+9+8=38.2
Количество пробиваемых полей Белые = 14 (пешки) + 4 (кони) = 18 (1.8 баллов)
Количество пробиваемых полей Черные = 14 + 4 = 18 (1.8 баллов)
Примечание. Пусть будет 0.1 балл за одно свободное поле под атакой.
Премия за очередь хода. Пусть пока будет 0. Не уверен, что это вообще хорошая идея.
Проверку на мат проводим. Вообще, вряд ли кому-то будет мат в начальной позиции или после первого полухода. Но проверять надо.
Оценка позиции = Белые - Черные = (38.2+18)-(38.2+18) = 56.2-56.2 = 0
Теперь нам надо подобным образом оценить все позиции после всех возможных ходов.
Оценка позиции после 1-го хода белых
Ход Баллы
a3 0.0
a4 0.2
b3 0.2
b4 0.2
c3 0.2
c4 0.3
d3 0.6
d4 0.7
e3 0.9
e4 0.9
f3 0.0
f4 0.1
g3 0.2
g4 0.2
h3 0.0
h4 0.2
Кa3 0.1
Кc3 0.3
Кf3 0.3
Кh3 0.1
Получается следующий результат. Если применять данную оценочную функцию и использовать глубину расчета на 1 полуход, то в данной позиции получаются лучшие ходы: e3 или е4.
Теперь мы можем уточнить оценку начальной позиции. Если изначально она была равна 0, то после первого полухода стала равной 0.9.
Разумеется, если мы посмотрим чуть глубже (т.е. оценим все позиции после всех возможных 2-х полуходов), то оценка начальной позиции опять изменится. Наверное, она опять станет равной 0, например, после 1. e4 e6.
А если посмотреть немного глубже, хотя бы на 20 полуходов? Все это, конечно, можно сделать, посвятив этому процессу месяц или два, но это уже всё сделано до нас.
...
Первоисточник:
===